Voici quelques notions de cosmographie (description de l’Univers planétaire) indispensables à l’Astrologue.

Tout le monde sait que la Terre est une boule presque sphérique isolée dans l’espace. Elle tourne sur elle-même en 24 heures sidérales, soit en 23 h 56 m environ du temps usuel. L’axe fictif, autour duquel la Terre tourne sur elle-même, s’appelle axe terrestre. Aux deux extrémités de cet axe se trouvent les pôles : Pôle Nord et Pôle Sud.

Le grand cercle — on appelle grand cercle celui qui partage une sphère en deux parties égales, un grand cercle passe obligatoirement par le centre de la sphère. La position de l’équateur est donc nettement définie, puisqu’il doit passer par le centre de la Terre et être perpendiculaire à l’axe terrestre — dont le plan est perpendiculaire à l’axe terrestre se nomme équateur terrestre. Les autres grands cercles, qui passent par les pôles, et qui peuvent s’orienter dans toutes les directions, sont désignés sous le nom de méridiens, leur nombre est infini et ils coupent toujours l’équateur à angle droit. Voir fig. 1

Pour situer un point quelconque à la surface de la Terre, on utilise les latitudes et les longitudes, les premières prenant comme point de départ l’équateur, les secondes partant d’un méridien conventionnel appelé couramment grand (ou premier) méridien terrestre. Ce méridien passait autrefois par l’observatoire de Paris, il passe actuellement par celui de Greenwich. La latitude terrestre ou géographique d’un lieu quelconque se définit ainsi : la distance de ce lieu à l’équateur, ou l’arc du méridien terrestre compris entre ce lieu et l’équateur, compté en degrés, minutes et secondes. La latitude est nord (ou boréale) ou bien sud (ou australe) suivant que le lieu considéré se trouve dans l’hémisphère nord ou dans l’hémisphère sud. Dans la fig. 1 l’arc de méridien AB mesure la latitude de la ville B, l’arc V’V celle de la ville V.

La longitude terrestre est l’angle du méridien du lieu avec un méridien origine (méridien de Greenwich) choisit arbitrairement. Elle est orientale ou occidentale suivant que le point est à l’Est ou à l’Ouest du méridien origine. Exemple : la latitude de Paris (Observatoire) est de 48° 50’ 11’’ nord, sa longitude est de 2° 20’ 14’’ 4’’’ Est de Greenwich. La longitude se mesure soit en degrés (de 0° à 180°, Est ou Ouest) soit en temps (de 0 heure à 12 heures Est ou Ouest). La latitude se compte toujours en degrés de 0° à 90°, Nord ou Sud. Ces coordonnées terrestres — latitude et longitude — sont indiquées à 30’’ près pour chaque chef-lieu de département. Dans la fig. 1 l’arc d’équateur OA mesure la longitude de Villes C, B et D ; l’arc OV’ celle de la ville V.

On peut aussi, en partant d’un point évaluer en kilomètres, sur une carte, la distance entre le premier point (dont la latitude et longitude sont connues) et le lieu dont on veut connaître la latitude ou la longitude.

Cela est facile, étant donné que toutes les cartes ou plans sont habituellement orientés dans la direction Nord-Sud. Prenons un exemple : on demande la latitude du palais de l’Elysée à Paris (latitude qu’il serait convenable d’utiliser pour tous les thèmes d’Astrologie mondiale, étant donné que c’est là que réside actuellement le chef de l’Etat). La latitude de l’Observatoire est 48° 50’ 11’’.

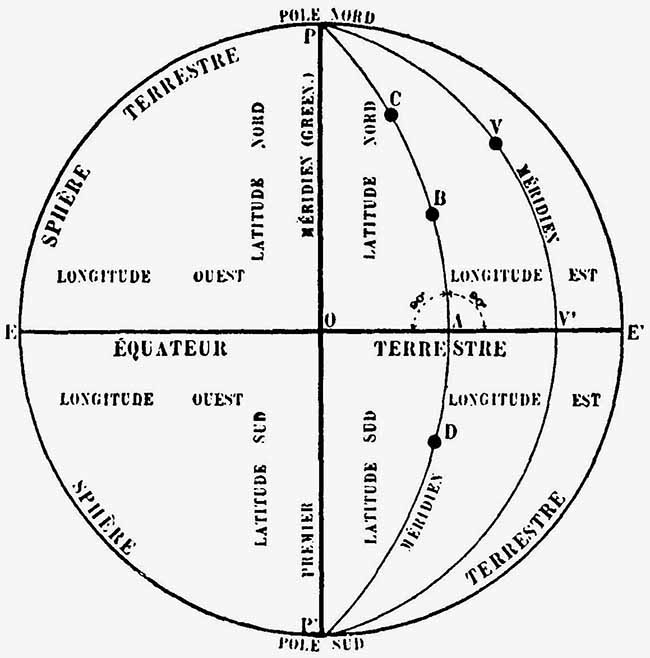
Fig. 1

La distance approximative entre un parallèle passant par ce point et un autre passant par l’Elysée (distance évaluée sur un plan) est de 3.820 mètres. En convertissant cette distance en minutes et secondes d’arc nous aurons la latitude de l’Elysée. La valeur d’un degré de latitude oscille entre 110.576 mètres à l’équateur et 111.700 mètres aux pôles. Pour nos régions cette valeur est de 111.038 mètres vers 40° de latitude ; de 111.135 pour 45°, de 111.214 pour 49° et de 111.233 pour 50°. Pour la latitude 48° 50’ la valeur d’un degré peut s’évaluer à 111.210 mètres de sorte qu’une minute vaut 1.853,50 m et une seconde 30,89 m. Les 3.820 mètres, trouvés plus haut correspondent donc à 2’ 4’’ d’arc environ et la latitude cherchée sera de 48° 52’ 15’’. Pour la longitude on peut procéder de la même manière mais ici la valeur de chaque degré de parallèle en mètres, est très variable, la voici pour les latitudes courantes :

Soit à déterminer la longitude des tribunes du champ de courses du Tremblay, point situé à 11.500 km environ à l’Est de l’Observatoire de Paris, nous aurons : valeur d’un degré sous cette latitude 73.250 mètres ; valeur d’une minute 1.221 mètres environ, ce qui donne 9’ 30’’ Est de Paris de 2° 29’ 54’’ est GR.
 
Quand on dresse une carte du ciel sans rechercher la précision, on peut se contenter d’évaluer la latitude et la longitude terrestres à quelques minutes, même à un demi-degré près. Mais si l’on désire un thème précis, pouvant servir de base au calcul des directions, il est indispensable d’évaluer la latitude à une minute près, car, ici, une négligence d’une trentaine de minutes peut, dans les directions, provoquer un écart de 6 mois, même un an. Quand la méthode du calcul des directions sera bien au point, il sera judicieux de pousser l’évaluation de la latitude à 10’’ près pour obtenir des arcs très précis, mais nous n’en sommes pas encore là.
 
Passons maintenant à la définition de quelques éléments célestes, mais, au préalable, notons qu’en Astrologie on considère la Terre comme le centre du monde et les mouvements apparents sont considérés comme réels.

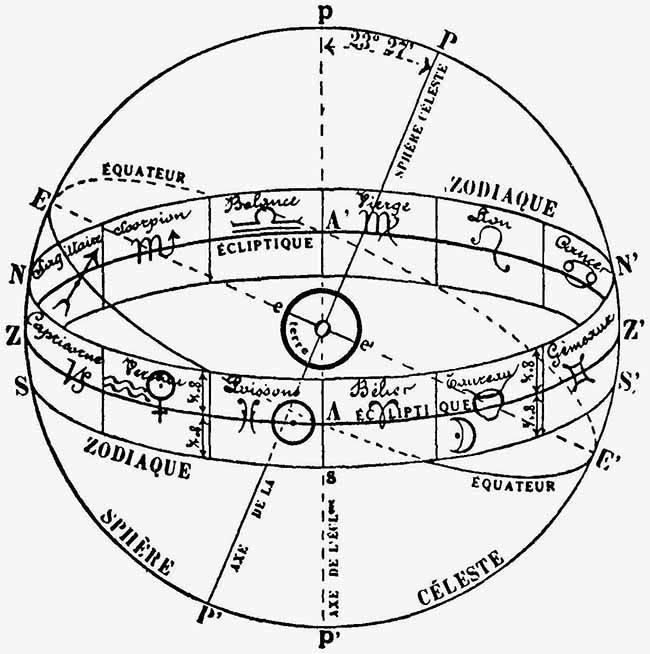
Fig. 2

Le Soleil, dans sa course (apparente) annuelle décrit une courbe presque circulaire, d’un rayon moyen de 149 millions de kilomètres en 365 jours 5 heures 49 minutes. Ce cercle décrit par le Soleil, c’est l’Ecliptique. Les autres planètes paraissent également décrire des cercles, semblables à celui décrit par le Soleil, appelés orbites. Il y a une orbite pour chaque planète et, vues de la Terre, ces orbites ne se différencient de celle du Soleil que par une inclinaison différente d’ailleurs minime puisqu’elle ne dépasse pas 8° et demi. On peut admettre, grosso-modo, que toutes les planètes se déplacent apparemment sur l’écliptique.

C’est pour cela qu’en Astrologie et en astronomie, l’écliptique joue un rôle capital : c’est le cercle qui sert de base aux coordonnées célestes. Mais avant de définir les diverses coordonnées utilisées couramment en Astrologie et astronomie nous devons dire deux mots du Zodiaque, que l’on confond souvent avec l’écliptique. Le Zodiaque est une bande circulaire, partagée en son milieu par l’écliptique. La largeur de cette bande est de 17° environ, soit 8° ½ de part et d’autre de l’écliptique. Voir figure 2 où le zodiaque est représenté par la bande NS N’S’, alors que l’écliptique est représentée par la ligne circulaire Z Z’. Toutes les planètes se meuvent apparemment dans les limites de cette bande puisque leur latitude maximum n’excède pas 8° ½. C’est d’ailleurs cette considération qui a fixé les dimensions de la largeur du zodiaque. Par contre un grand nombre d’étoiles sont en dehors de la « bande » zodiacale. Comme l’écliptique représente la marche apparente du Soleil, il s’ensuit que ce cercle se trouve nettement orienté, dans l’espace, et par conséquent l’orientation du zodiaque se trouve aussi nettement définie. Pour éviter toute confusion entre écliptique et zodiaque il suffit donc de se rappeler que la première est une ligne circulaire, alors que le second est une zone circulaire de 17° de largeur [1].

Le zodiaque se divise en 12 secteurs ou signes zodiacaux appelés le Bélier, le Taureau, etc., voir figure 2. Bien remarquer que ces signes sont tous égaux (30°), alors que les constellations portant les mêmes noms (Bélier, Taureau, etc.) sont des zones célestes renfermant un certain nombre d’étoiles principales. C’est ainsi que la constellation du Taureau s’étend sur plus de 40° de longitude.

Pour dresser une carte du ciel, il est indispensable de connaître la position d’une planète dans le zodiaque, pour cela on se sert des éphémérides, qui donnent la position des planètes pour chaque jour. Lorsqu’un astre se trouve exactement sur l’écliptique (voir le Soleil dans la fig. 2) on dit qu’il n’a pas de latitude céleste. Lorsqu’une planète se trouve en dessus (voir Vénus dans la fig. 2) elle possède une latitude Nord ; et si la planète est en dessous (voir la Lune dans la même figure), sa latitude est Sud. Dans notre figure la latitude de la Lune serait de 4° ½ Sud environ, et celle de Vénus 4° ½ Nord. La position d’une planète (longitude), dans le zodiaque, se mesure à partir du point vernal (point A, dans la figure), qui sera défini plus loin. Cette longitude se mesure soit en degrés, de 0° à 360°, soit en signes. C’est ainsi que pour la Lune (fig. 2) on pourra dire que sa longitude est de 35° (environ) ou bien : la Lune se trouve à 5° du Taureau. Pour le Soleil la longitude (mesurée sur le cercle A Z’ A’ Z-Soleil) sera de 355° ou 25° des Poissons. Pour Vénus nous dirons qu’elle est à 315° ou 15° du Verseau. La conversion des degrés exprimés en longitudes, en degrés exprimés en signes, se fait aisément à l’aide du « graphique zodiacal » utilisé pour les thèmes. On verra aisément sur ces graphiques que le degré 180° correspond à 0° de la Balance que le 334° correspond à 4° des Poissons, etc.

C’est la distance qui sépare une planète d’une autre, qui nous renseigne si ces deux astres sont en aspect ou non.

Les notions très sommaires qui précèdent seraient suffisantes, à la rigueur, pour comprendre le mécanisme de l’établissement d’une carte du ciel, en ce qui concerne la position des planètes, tout au moins. Pour donner une idée sommaire des maisons nous dirons tout de suite qu’elles ont pour objet de nous renseigner si, au moment de la naissance, tel ou tel astre, se trouvait dans la partie visible du ciel (sur l’horizon), ou dans la partie invisible (sous l’horizon). Les planètes qui sont dans le voisinage de la maison X, sont celles qui sont les plus élevées dans le ciel, celles dont les rayons se rapprochent le plus de la verticale du lieu de naissance, ce sont donc les planètes les plus efficaces. Par contre les rayons des planètes qui sont sous l’horizon ne peuvent nous influencer qu’après avoir traversé la Terre. Ceci explique l’utilité des maisons.

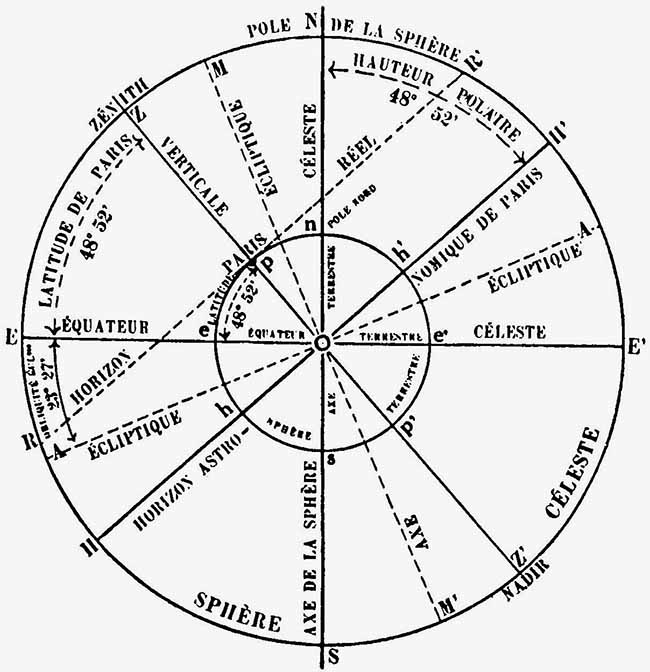
Fig. 3

Après ces notions très sommaires, nous allons entrer dans des définitions un peu plus précises, un peu plus scientifiques, en faisant remarquer que les notions suivantes ne sont pas indispensables à l’interprétation correcte d’une carte du ciel. Par contre elles sont indispensables pour comprendre le mécanisme des directions primaires, ou pour comprendre la domification.

Sphère céleste : La sphère céleste est une sphère idéale, ayant la Terre pour centre, de rayon arbitraire, mais suffisamment grand pour que la Terre, comparée à cette sphère, puisse être considérée comme un simple point. La sphère céleste est en quelque sorte une copie immensément agrandie de la sphère terrestre. L’axe de la sphère céleste NS (Voir fig. 3) se trouve sur le prolongement de l’axe terrestre ns ; le plan de l’équateur céleste EE’ se trouve sur le prolongement du plan de l’équateur ee’. L’orientation de notre sphère est donc parfaitement définie par ce qui précède. Le pôle nord de la sphère se trouve en N, sur le prolongement de l’axe terrestre, et dans la même direction que notre Pôle Nord. Le Pôle Sud se trouve en S.

L’inclinaison du plan de l’écliptique AA’, n’est pas la même que celle du plan de l’équateur céleste EE’, ces deux plans forment par leur intersection un angle dièdre de 23° 27’ environ (arc EA) appelé obliquité de l’écliptique. De même l’axe de la sphère céleste NS forme avec l’axe de l’écliptique — MM’ — un angle de 23° 27’. M et M’ sont les deux pôles de l’écliptique.

Cercles de longitude, cercles d’ascension droite : les grands cercles qui passent par les pôles de l’écliptique sont appelés cercles de longitude, ou bien cercles de latitude. Ce sont ces cercles qui servent à mesurer la longitude des astres, et c’est sur ces cercles que se mesure la latitude des mêmes.

Les grands cercles passant par les pôles de la sphère sont dits cercles d’ascension droite (cercles d’AR), ou bien cercles de déclinaison. Ils servent à mesurer l’AR des astres, et c’est sur ces mêmes cercles que se mesure la déclinaison (Voir fig. 4).

Point gamma ou point vernal : pour mesurer une longitude ou une AR il faut évidemment, comme nous l’avons vu pour la Terre, prendre un point de départ, choisir en quelque sorte un méridien origine. Ce point de départ est le même pour l’écliptique et pour l’équateur céleste. Le méridien origine des longitudes célestes et des AR passe par les deux intersections que forment les cercles « écliptique » et « équateur céleste », voir figure 2. On a choisi l’intersection qui est occupée par le Soleil au moment où commence le printemps (pour les latitudes Nord). C’est donc à partir du point vernal (ou équinoxe de printemps, ou 0° du Bélier) que se comptent les longitudes et les AR que nous allons maintenant définir.
 
Longitudes (Long.) et Ascensions droites (AR) : la longitude se définit ainsi : arc d’écliptique compris entre le point vernal et le point où le cercle de longitude, de l’astre considéré, coupe l’écliptique. Si l’astre se trouve sur l’écliptique même ; on peut simplifier ainsi la définition : nombre de degrés, minutes et secondes, de l’écliptique, compris entre le point vernal et le centre de l’astre envisagé.

Dans la figure 4 les cercles de longitude sont dessinés en traits pleins. La longitude du Soleil est donc représentée par l’arc d’écliptique YS. L’arc LY indique la distance en longitude qui sépare l’étoile e du point vernal (Y). L’arc YR représenterait la longitude de n’importe quel astre situé sur le demi-cercle PRP’.
 
L’ascension droite est l’arc d’équateur compris entre le point vernal et le cercle d’AR passant par le centre de l’astre. Dans la figure 4, l’AR du Soleil est représenté par l’arc Ys ; l’AR du point R sera indiqué par l’arc Yr. La longitude de l’étoile e se mesure au point L tandis que son AR se mesure au point A. L’AR d’un point quelconque de l’écliptique — par exemple a — se mesurera en faisant passer par le point considéré un cercle d’AR. Dans l’exemple précité l’AR se mesurera au point A.

Latitude et déclinaison : la latitude céleste est la distance qui sépare le centre d’un astre du plan de l’écliptique ; cette distance devant se mesurer sur le cercle de longitude. Dans la figure 4 la latitude de l’étoile e est représentée par l’arc Le. La latitude du point A est représentée par l’arc BA.

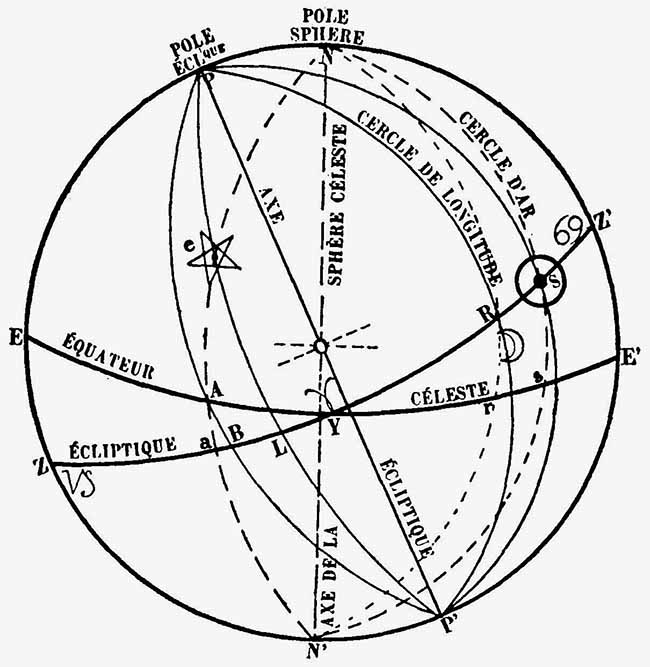
Fig. 4

La déclinaison est l’arc de cercle d’AR compris entre le centre de l’astre et l’équateur céleste. Dans la figure 4 l’arc sS représente la déclinaison du Soleil. Cet arc représente également la déclinaison du point S de l’écliptique. La déclinaison de l’étoile e sera l’arc Ae.

La latitude et la déclinaison sont Nord ou Sud suivant qu’elles se mesurent dans l’hémisphère Nord ou dans l’hémisphère Sud, par rapport aux plans respectifs de l’équateur et de l’écliptique. Dans la figure 4 l’étoile e possède une latitude Nord et une déclinaison Nord. Le Soleil a une déclinaison Nord et il n’a pas de latitude ; la Lune, sur notre figure, possède une latitude Sud et une déclinaison Nord.

Pratiquement, pour dresser un thème, la latitude, la longitude et la déclinaison des planètes se calculent d’après les éphémérides, l’AR se détermine à l’aide de tables spéciales ou d’une formule trigonométrique. La déclinaison sert à déterminer les aspects parallèles. L’AR sert à calculer les directions primaires. La latitude n’est guère utilisée pratiquement, bien qu’elle possède une signification, d’après certains auteurs [2].

Verticale, Méridien, Horizon : La verticale, en un lieu quelconque, est indiquée par la direction du fil à plomb. Dans la figure 3, Zp0 représente la verticale du point p (Paris). Les points Z et Z’ représentent le Zénith et le Nadir du point p. On confond parfois zénith avec MC. Il y a pourtant une différence importante : le zénith est sur la verticale du lieu, tandis que le MC se situe sur l’écliptique, qui, sous nos latitudes, ne passe jamais au zénith. Pour les latitudes comprises entre 23° 27’ Nord et 23° 27’ Sud il peut y avoir concordance entre le MC et le zénith.

Le méridien d’un lieu quelconque, est un grand cercle de la sphère céleste passant à la fois par les pôles de la sphère et par le zénith du lieu considéré. Dans la figure 5 le grand cercle ZHZ’H’ figure le méridien. On confond également, parfois, méridien et MC ; la différence est pourtant considérable : le méridien est un grand cercle alors que le MC est le point qui se trouve à l’intersection du méridien et de l’écliptique. Dans la figure 5 le MC se trouve à 0° du Bélier (au point Y). Le point d’intersection opposé c’est le FC (point Y’ sur la figure).

On appelle premier vertical, un grand cercle de la sphère passant par le zénith, mais perpendiculaire au cercle méridien et perpendiculaire, également à l’horizon. Le premier vertical ne passe donc pas par les pôles de la sphère. (Voir fig. 5). Ce cercle est utilisé pour la domification dans la méthode de Campanus et pour calculer les directions dans certaines méthodes.

L’horizon réel d’un lieu est un plan horizontal (ou perpendiculaire à la verticale) passant par ce lieu. Dans la figure 3 la ligne RR’ indique l’horizon réel de Paris.

L’horizon astronomique est un plan parallèle à l’horizon réel, mais passant par le centre de la terre. Dans la figure 3, HH’ indiquent l’horizon astronomique de Paris. Pratiquement, comme la Terre est considérée (dans les calculs) comme un point, l’horizon réel et l’horizon astronomique se confondent. Dans notre figure nous avons évidemment exagéré les dimensions par rapport à celles de la sphère céleste, ce qui provoque une différence énorme entre l’horizon réel et l’horizon astronomique.

L’intersection formée par l’horizon avec l’écliptique indique la position de l’AS et de l’OCC dans le thème. Dans la figure 5 on voit que le cercle horizon coupe l’écliptique vers la fin du signe du Cancer, c’est ce point (AS sur la figure) qui constitue le degré Ascendant, ou Horoscope.

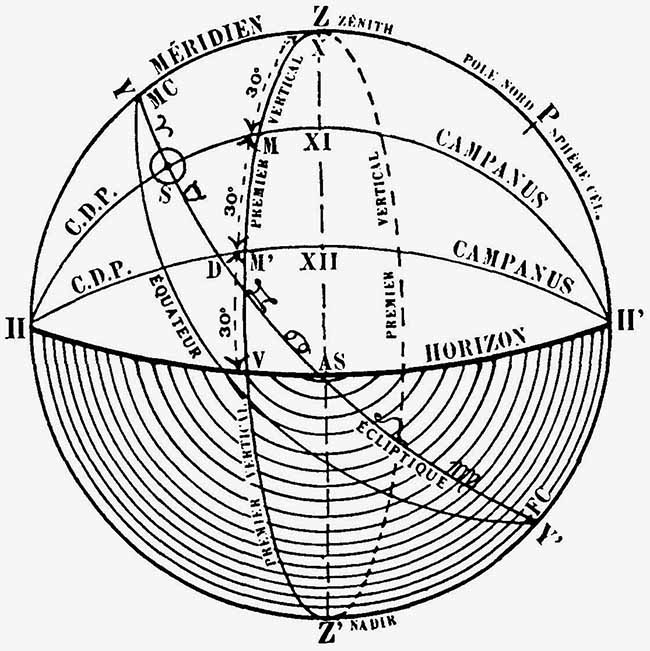
Fig. 5

Hauteur polaire, Cercle de position : On appelle hauteur polaire, d’un lieu quelconque, l’angle que forme l’horizon de ce lieu avec le pôle visible de la sphère (pôle nord, sous nos latitudes). Dans la figure 3, l’arc NH’ indique la hauteur polaire de Paris. Cette dernière est toujours équivalente à la latitude géographique du lieu de naissance. En effet si dans notre figure 3 nous déplaçons notre verticale du point Z pour la ramener vers E (en modifiant successivement notre lieu d’observation), nous constatons que HH’ (toujours perpendiculaire à la verticale) suivra ce même mouvement, et H’ se rapprochera de plus en plus de N, de sorte que, plus notre latitude géographique sera faible, plus la hauteur polaire deviendra également faible. Lorsque notre lieu d’observation sera au point e (sur l’équateur terrestre) la verticale du lieu sera OE et l’horizon sera SN, donc la hauteur polaire sera également nulle, comme la latitude géographique.

La définition du cercle de position présente deux variantes, suivant la méthode de domification adoptée. Pour Regiomontanus et Campanus, les cercles de position (CDP) sont de grands cercles de la sphère passant par les deux intersections de l’horizon et du méridien (ces deux cercles se coupent à angle droit) et par le centre d’un astre quelconque, (ou point du ciel). Dans la figure 5 le demi-cercle HMH’ représente la moitié du cercle de position du Soleil. L’orientation du cercle de position est ici définie par quatre points : le centre de la sphère, le centre de l’astre et les deux intersections du méridien et de l’horizon (H et H’ sur la figure).

Pour Placidus, le cercle de position d’un astre quelconque, passe toujours par le centre de cet astre, mais il ne passe pas obligatoirement par les intersections du méridien et de l’horizon, mais bien par un certain point situé sur l’équateur. La distance de ce point à l’horizon, doit être proportionnelle au parcours effectué par l’astre sur son semi-arc. Par exemple si un astre a parcouru les 2/3 de son SA, la distance du point situé sur l’équateur, sera également aux 2/3 de l’arc d’équateur compris entre l’horizon et le méridien. Supposons un astre au point i (fig. 6) et ayant, par conséquent parcouru sur son parallèle à l’équateur — P’hiP — la partie ih de son SA ; le cercle de position de ce point i, dans la méthode Placidus devra passer par un point t, et la distance tD, par rapport à tY, devra être proportionnelle à ih par rapport à iP. La détermination de ce point t se fait à l’aide de la relation suivante :

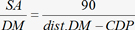
ce qui donne :

Les CDP servent à deux choses :

• pour effectuer la « domification » ;
• pour calculer les directions primaires.

Arcs, semi-arcs, différence ascensionnelle, distance méridienne : On appelle arc diurne : le temps pendant lequel un astre est visible. Arc nocturne le temps pendant lequel il est invisible. Les arcs se mesurent soit en degré d’AR soit en heures. Dans les calculs astrologiques on utilise le serai-arc (SA) qui est la moitié de l’arc. Dans la figure 6 l’astre i, suit dans son mouvement diurne le parallèle [3] P’hiP. Son semi-arc diurne est représenté par l’arc d’équateur YA. Son semi-arc nocturne par AY’.

La différence ascensionnelle (DA) est le temps mis par un astre, en plus ou en moins de 6 heures, pour parcourir son semi-arc. Ou bien le temps que met un astre, en plus ou moins de six heures, depuis son passage à l’horizon, pour atteindre le méridien du lieu de naissance. Dans la figure 6 l’arc d’équateur DA représente la différence ascensionnelle (DA) du point h pour la hauteur polaire de Paris (approximativement). En ajoutant à 90° la DA, ou bien en retranchant la DA de 90°, on obtient le semi-arc. La DA est fonction à la fois de la LG du lieu de naissance et de la déclinaison de l’astre (ou point du ciel) envisagé. Elle se calcule soit à l’aide de tables appropriées, ou à l’aide d’une formule trigonométrique.

La distance méridienne (DM) d’un astre est l’arc d’équateur compris entre l’astre considéré et le méridien inférieur ou supérieur. En d’autres termes c’est la différence en AR, entre l’AR du MC et l’AR de l’astre. Dans la figure 6 la DM du point h c’est l’arc AY.

Les SA et DM servent aux calculs des directions et à la domification.

Mouvement diurne : si par une belle nuit, nous observons le ciel, et en particulier, pour plus de facilité, la marche de la Lune, nous remarquerons que celle-ci nous apparaît du côté du levant, pour s’élever progressivement jusqu’à ce qu’elle ait atteint sa hauteur maximum (passage au méridien), et ensuite nous la verrons décliner, pour disparaître à l’Ouest, environ une douzaine d’heures après son lever. Si nous observons les étoiles qui se trouvent dans le voisinage de la Lune nous remarquerons aussi qu’elles accompagnent la Lune dans sa course céleste. En fait tout le ciel nous paraît tourner autour de nous, d’Est en Ouest. C’est ce qu’on appelle le mouvement diurne. Mouvement fictif, engendré par la rotation réelle de la Terre dans le sens contraire, d’Ouest en Est. Cette notion de mouvement diurne est prise en considération dans la domification « placidienne » et partant dans le calcul des directions.

Domification : La domification est en quelque sorte un partage de l’écliptique et 12 sections différentes et d’étendue variable. Elle a pour but de déterminer l’orientation des astres, par rapport au lieu d’observation, cette orientation devant jouer un rôle capital quant à l’influence des mêmes. L’expérience démontre en effet que l’action d’un astre varie suivant qu’il se trouve plus ou moins élevé par rapport à l’horizon, plus ou moins éloigné du méridien, etc. Tous les astrologues sont à peu près d’accord sur la division du ciel en 12 maisons, nombre correspondant aux signes zodiacaux. Ceci permet d’ailleurs d’établir une analogie entre les signes et les maisons.

Par contre il existe plusieurs méthodes de domification [4]. Ici nous ne retiendrons que les trois principales : la méthode Campanus, la méthode Regiomontanus et la méthode Placidus. Disons tout de suite que la méthode Placidus est universellement employée, à l’heure actuelle, et cela tient à ce qu’il existe des « tables des maisons », établies suivant cette méthode, et évitant tout calcul fastidieux. Nous ferons cependant remarquer que les astrologues du XV-XVII^ème siècle ont presque toujours utilisé la méthode Regiomontanus, avec laquelle Morin, notamment, a obtenu de très bons résultats. De nos jours cette méthode paraît revenir en vogue, surtout en Allemagne, et on peut se demander si elle ne va pas s’imposer à nouveau à l’attention des astrologues.

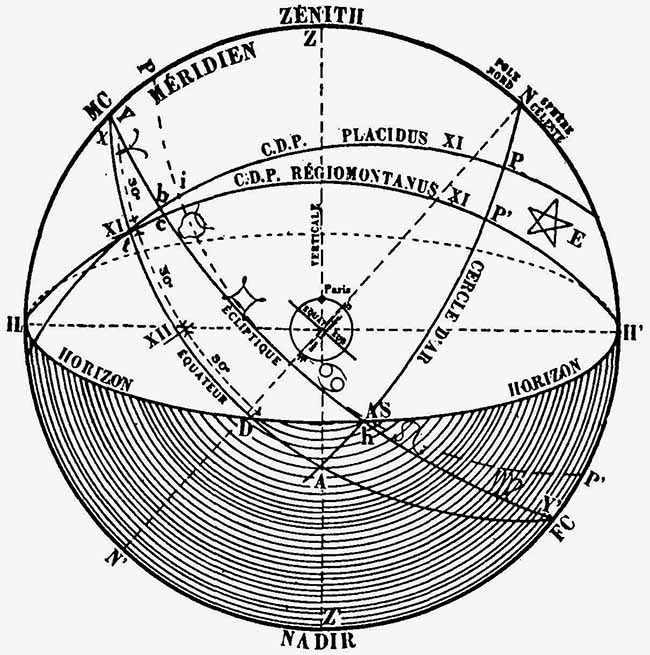
Fig. 6

Pour simplifier le problème de la domification, il faut d’abord remarquer que dans les trois méthodes ci-dessus, la position des angles du thème (MC-FC-AS-OCC) se détermine de la même manière. Les intersections du méridien et de l’horizon avec l’écliptique déterminent toujours la position de ces quatre angles du thème. Ce n’est donc que pour les maisons intermédiaires, XI, XII, II, III — et les pointes opposées — qu’il y a divergence. Pour déterminer ces maisons intermédiaires, par exemple les pointes de XI et XII, dans la méthode Campanus on divise les 90° de l’arc ZMM’V’ (voir fig. 5) du premier vertical, compris entre l’horizon oriental et le méridien, en trois parties égales et par ces points M et M’ on fait passer les cercles de position (qui doivent, ne l’oublions pas, passer par les intersections HH’ de l’horizon avec le méridien). Les points S et D’ où ces cercles traversent l’écliptique, constituent les pointes de XI et XII (voir fig. 5). Pour les maisons II et III on procède d’une manière similaire en divisant l’arc VZ’.

Dans la méthode Regiomontanus (fig. 6) on divise en 3 l’arc d’équateur YD compris entre le méridien et l’horizon. On fait passer l’arc des CDP par ces points XI et XII et les cuspides des maisons se déterminent comme plus haut. Dans la figure 6 la pointe de XI se trouve en C. Le CDP de la maison XII n’est pas tracé.

Dans la méthode de Placidus on divise également l’arc d’équateur YD (entre le méridien et l’horizon), comme chez Regiomontanus, mais ici comme les CDP ne passent plus par les intersections du méridien et de l’horizon mais bien par un certain point situé sur l’écliptique, et déterminé par des approximations successives, il s’ensuit que le CDP coupe l’écliptique en un point différent.

Dans la figure 6 les CDP de Placidus et de Regiomontanus passent tous les deux par le point T, mais comme leur orientation n’est pas la même, la pointe de la maison XI vient se situer pour Placidus en b (et non en c, comme pour Regiomontanus). L’étoile E se trouve dans un cas en maison X et dans l’autre en maison XI. (Sur notre figure l’écartement des CDP se trouve évidemment exagéré).

Il nous reste à définir le pôle d’une planète, ou d’une pointe de maison. On appelle ainsi l’élévation du pôle visible de la sphère au-dessus du CDP de la planète ou de la cuspide considérée. Dans la figure 6 l’élévation du pôle de XI serait indiquée par l’arc NP, pour la domification Placidienne, et par l’arc NP’ pour Regiomontanus, si nous supposons les arcs NP NP’ perpendiculaires aux CDP, ce qui n’est pas le cas dans notre figure. L’arc NH’ représente, dans les deux méthodes, le pôle (ou hauteur polaire) de l’AS, égal à la latitude géographique.